In the given figure, ABCD is a square and ![]() If PB = QC = DR, prove that
If PB = QC = DR, prove that
(i) ![]() (ii)
(ii) ![]()
(iii) ![]()
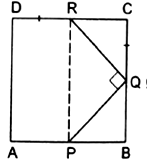
Given: ABCD is where ![]() and
and ![]()
To prove: (i) ![]() (ii)
(ii) ![]()
(iii) ![]()
Proof:
(i) Here,
BC = CD …Sides of square
CQ = DR …Given
BC = BQ + CQ
∴ CQ = BC − BQ
∴ DR = BC – BQ ...(1)
Also,
CD = RC+ DR
∴ DR = CD − RC = BC − RC ...(2)
From (1) and (2), we have,
BC − BQ = BC − RC
∴ BQ = RC
(ii) Now in ∆RCQ and ∆QBP, we have,
PB = QC …Given
BQ = RC …from (i)
∠RCQ = ∠QBP …90° each
Hence by SAS congruence rule,
∆RCQ ≅ ∆QBP
∴ QR = PQ …by cpct
(iii) ∆RCQ ≅ ∆QBP and QR = PQ … from (ii)
∴ In ∆RPQ,
∠QPR = ∠QRP = ![]() (180° − 90°) =
(180° − 90°) = ![]() = 45°
= 45°
∴ ∠QPR = 45°
8