Prove that the sum of all the angles of a quadrilateral is 360°.

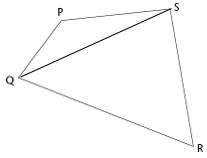
Given: Consider a PQRS where QS is diagonal.

To prove: ∠P + ∠Q + ∠R + ∠S = 360°

Proof:

For ∆PQS, we have,

∠P + ∠PQS + ∠PSQ = 180° ... (1) …Using Angle sum property of Triangle

Similarly, in ∆QRS, we have,

∴ ∠SQR + ∠R + ∠QSR = 180° ... (2) …Using Angle sum property of Triangle

On adding (1) and (2), we get

∠P + ∠PQS + ∠PSQ + ∠SQR + ∠R + ∠QSR = 180° + 180°

∴ ∠P + ∠PQS + ∠SQR + ∠R + ∠QSR + ∠PSQ = 360°

∴ ∠P + ∠Q + ∠R + ∠S = 360°

∴ The sum of all the angles of a quadrilateral is 360°.