In the adjoining figure, ![]() is a parallelogram in which
is a parallelogram in which ![]() If the bisectors of
If the bisectors of ![]() and
and ![]() meet
meet ![]() at
at ![]() prove that
prove that
(i) ![]() (ii)
(ii) ![]() and
and ![]() (iii)
(iii) ![]()
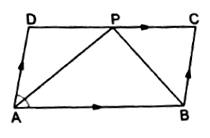
Given: ABCD is a parallelogram. The bisectors of ![]() and
and ![]() meet
meet ![]() at
at ![]() .
.
To prove: (i) ![]() (ii)
(ii) ![]() and
and ![]() (iii)
(iii) ![]()
Proof:
∴ ∠A = ∠C and ∠B = ∠D … Opposite angles
And ∠A + ∠B = 180° … Adjacent angles
∴ ∠B = 180° − ∠A
180° − 60° = 120° … as ∠A = 60°
∴ ∠A = ∠C = 60° and ∠B = ∠D = 120°
(i) In ∆ APB,
∠PAB = ![]() = 30°and ∠PBA =
= 30°and ∠PBA = ![]() = 60°
= 60°
∴ ∠APB = 180° − (30° + 60°) = 90°
(ii) In ∆ ADP, ∠PAD = 30° and ∠ADP = 120°
∴ ∠APB = 180° − (30° + 120°) = 30°
Hence,
∠PAD = ∠APB = 30°
Hence, ∆ADP is an isosceles triangle and AD = DP.
In ∆ PBC,
∠ PBC = 60°
∠ BPC = 180° − (90° +30°) = 60°and∠ BCP = 60° …Opposite angle of ∠A
∴ ∠ PBC = ∠ BPC = ∠ BCP
Hence, ∆PBC is an equilateral triangle and, therefore, PB = PC = BC.
(iii) DC = DP + PC
From (ii), we have
DC = AD + BC …AD = BC
DC = AD + AD
DC = 2 AD