In the adjoining figures, is a square. A line segment cuts at and the diagonal at such that and Find the value of

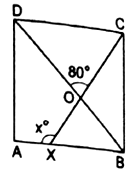
Here, ABCD is square.

Here AC and BD are diagonals.

We know that the angles of a square are bisected by the diagonals.

∴ ∠​OBX = 45° ∵∠​ABC = 90° and BD bisects ∠​ABC​
And ∠​BOX = ∠COD = 80° … Vertically opposite angles
∴​ In ∆BOX, we have:
∠AXO = ∠OBX + ​∠BOX … Exterior angle theorem
⇒​ ∠AXO = 45° + 80° = 125°
∴ ​x =125°