In the adjoining figures, is a parallelogram in which the bisectors of and intersect at a point Prove that

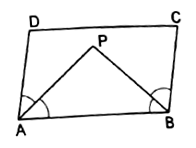
ABCD is parallelogram.

We know that the sum of the adjacent angles in parallelogram is 180°

∴ ​∠ A + ∠B = 180°

∴ + = = 90°

In ∆​ APB, we have:
∠​PAB = ∠A​ /2
∠​PBA = ∠B​ /2​
∴ ∠​APB = 180 − (∠​PAB​ + ∠​PBA) …Angle sum property of triangle
∴ ​∠APB = 180 – ( + )
∴ ∠APB = 180 − 90 = 90°
Hence, proved.