In the adjoining figures, is a parallelogram in which is produced to so that Prove that bisects

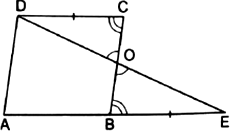
ABCD is parallelogram.

In ∆ODC and ∆​OEB, we have,
DC = BE …as DC = AB
∠COD = ∠BOE … Vertically opposite angles are equal
∠OCD = ∠OBE … Alternate angles with transversal BC
Hence, by SAA test for congruency, we get,
∆​ODC ≅ ∆​OEB

∴ OC = OB …by cpct
We know that BC = OC + OB.
∴ ED bisects BC.