In the adjoining figure, is a parallelogram. is the midpoint of and through a line segment is drawn parallel to to meet produced at and it cuts at Prove that

(i) (ii)

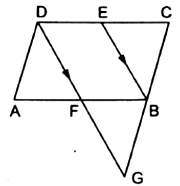
ABCD is parallelogram.

(i) In ∆​ DCG, we have:

DG || EB
DE = EC … E is the midpoint of DC)
Also, GB = BC … by midpoint theorem
∴​ B is the midpoint of GC.
Also, GC = GB + BC
GC = 2BC

GC =​ 2 AD …as AD = BC

∴ AD = GC

(ii) Now, in ∆​ DCG, DG || EB and E is the midpoint of DC and B is the midpoint of GC.

∴ EB = DG … by midpoint theorem

∴ DG = 2 EB