Show that the quadrilateral formed by joining the midpoints of the pairs of adjacent sides of a rhombus is a rectangle.

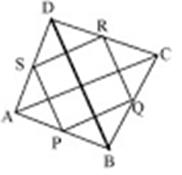
In ΔABC, P and Q are mid points of AB and BC respectively.
∴ PQ|| AC and PQ = 1/2AC … (1) …Mid point theorem
Similarly in ΔACD, R and S are mid points of sides CD and AD respectively.
∴ SR||AC and SR = 1/2AC …(2) …Mid point theorem
From (1) and (2), we get
PQ||SR and PQ = SR
Hence, PQRS is parallelogram ( pair of opposite sides is parallel and equal)

Now, RS || AC and QR || BD.

Also, AC ⊥ BD … as diagonals of rhombus are perpendicular bisectors of each other.

∴RS ⊥ QR.

Thus, PQRS is a rectangle.

Hence, the quadrilateral formed by joining the midpoints of the pairs of adjacent sides of a rhombus is a rectangle.