In the given figure, is a quadrilateral whose diagonals intersect at right angles. Show that the quadrilateral formed by joining the midpoints of the pairs of adjacent sides is a rectangle.

Question

Philoid · Accepted Answer

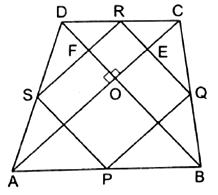
Here, in ABCD, diagonals intersect at 90°

Also, in ABCD, P, Q, R and S be the midpoints of AB, BC, CD and DA, respectively.

In ∆ ABC, we have,
∴ PQ ∣∣ AC and PQ = AC …by midpoint theorem

Similarly, in ∆DAC,

SR ∣∣ AC and SR = AC …by midpoint theorem

Now, PQ ∣∣ AC and SR ∣∣ AC

∴ PQ ∣∣ SR

Also, PQ = SR = AC

Hence, PQRS is parallelogram.

We know that the diagonals of the given quadrilateral bisect each other at right angles.
∴ ∠ EOF = 90°
Also, RQ ∣∣ DB
∴ RE ∣∣ FO
Also, SR ∣∣ AC
∴ FR ∣∣ OE
∴ OERF is a parallelogram.

So, ∠FRE = ∠EOF = 90° …Opposite angles of parallelogram are equal
Thus, PQRS is a parallelogram with ∠R = 90^o.
∴ PQRS is a rectangle.