Prove that the diagonals of a rhombus bisect each other at right angles.

Question

Philoid · Accepted Answer

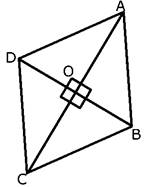
Let ABCD be a rhombus whose diagonal AC and BD intersect at the point O.

As we know that the diagonals of a parallelogram bisect each other and rhombus is a parallelogram.

So, OA=OC and OB=OD.

From ∆ COB and ∆ COD we get,

CB = CD (sides of rhombus) and

CO is common in both the triangles.

So, OB = OD

Therefore, by SSS theorem.

∆ COB ≅ ∆ COD

COB = COD

COB + COD = 180° (Linear pair of angles)

Thus, COB = COD = 90°

Hence, the diagonals of a rhombus bisect each other at right angles.