The bisectors of two adjacent angles of a parallelogram intersect at

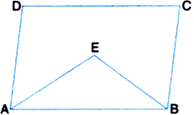
Let ABCD is a parallelogram.

The angle bisectors AE and BE of adjacent angles A and B meet at E.

AD || BC (Opposite sides of ||gm)

∠DAB + ∠CBA = 180°

2∠EAB + 2∠EBA = 180° (sum of the interior angles, formed on the same side of the transversal, is 180°)

AE and BE are the bisectors of ∠DAB and ∠CBA respectively.

∠EAB + ∠EBA = 90° ... (1)

In ∆EAB,

∠EAB + ∠EBA + ∠AEB = 180° (sum of the angles of a triangle is 180°)

90° + ∠AEB = 180°

From (1)

∠AEB = 90°