(a) Draw a ray diagram to show the formation of image by a convex lens when an object is placed in front of the lens between its optical centre and principal focus.

(b) In the above ray diagram mark the object-distance (u) and the image-distance (v) with their proper signs (+ve or -ve as per the new Cartesian sign convention) and state how these distances are related to the focal length (f) of the convex lens in this case.

(c) Find the power of a convex lens which forms a real, and inverted image of magnification -1 of an object placed at a distance of 20 cm from its optical centre.

(a)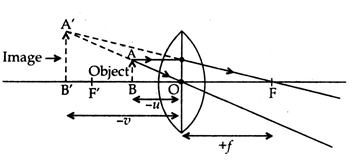

The image formed is – behind the object (on the left side of lens)

- Virtual and erect

- Larger than the object

(b) According to the new Cartesian sign convention the following are the rules-

(i) All the distances are measured from the optical centre of lens

(ii) The distances measured in same direction as that of incident light are taken positive.

(iii) The distances measured against the direction of the incident light are taken negative.

(iv) The distances measured upwards and perpendicular to the principal axis are taken positive, others negative.

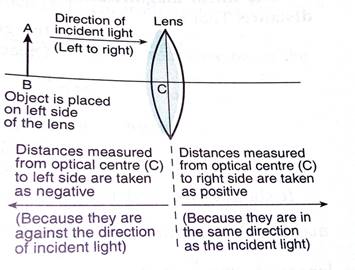
The focal length of convex lens is considered positive, for concave lens it is negative.

The relation between u, v and f is given by the lens formula

As both (u) and (v) are negative, the above equation will change to:

(c) given u= -20cmm = -1

magnification m= v/u

→ v=mu

→ = -1 × -20 = 20cm

Thus, v = 20 cm

Now, focal length is given as:

→

→ f = 10cm

Now, we know,

→

→ P = 10 D