In the given figure, O is the centre of a circle in which ∠OBA = 20° and ∠OCA = 30°. Then, ∠BOC = ?

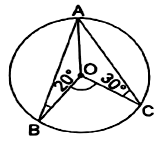
Given: and

Consider ΔOAB

Here,

OA = OB (radius)

∠OBA = ∠OAB = 20° (angles opposite to equal sides are equal)

By angle sum property

∠AOB + ∠OBA + ∠OAB = 180°

∠AOB + 20° + 20° = 180°

∠AOB = 180° – 20° – 20°

∠AOB = 140°

Similarly, in ΔAOC

OA = OC (radius)

∠OCA = ∠OAC = 30° (angles opposite to equal sides are equal)

By angle sum property

∠AOC + ∠OCA + ∠OAC = 180°

∠AOC + 30° + 30° = 180°

∠AOC = 180° – 30° – 30°

∠AOC = 120°

Here,

∠CAB = ∠OAB + ∠OAC = 50°

Here,

2CAB = BOC (The angle subtended by an arc at the center is twice the angle subtended by the same arc on any point on the remaining part of the circle).

2CAB = BOC

2 × 50° = BOC

BOC = 100°.

BOC = 100