In the given figure, ABCD is a cyclic quadrilateral in which DC is produced to E and CF is drawn parallel to AB such that ∠ADC = 90° and ∠ECF = 20°. Then, ∠BAD = ?
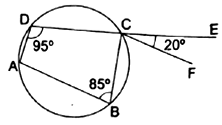
Given: ![]() is a cyclic quadrilateral, CF||AB,
is a cyclic quadrilateral, CF||AB, ![]() and
and ![]()
Here, CF|| AB
Hence BC is transversal
∴ ∠ABC = ∠BCF = 85° (Alternate interior angles)
Here,
∠DCB + ∠BCF + ∠ECF = ∠DCE
∠DCB + 85° + 20° = 180°
∠DCB = 180° – 85° – 20° = 75°
We know that,
In a cyclic quadrilateral opposite angles are supplementary
∴ ∠DCB + ∠BAD = 180°
75° + ∠BAD = 180°
∠BAD = 180° – 75° = 105°
∴ ∠BAD = 105°
39