In ∆ABC, if D is the midpoint of BC and E is the midpoint of AD, then ar(∆BED) = ?

Question

Philoid · Accepted Answer

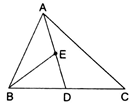
Given: D is the midpoint of BC and E is the midpoint of AD

Here,

D is the midpoint of BC and AD is the median of ΔABC

Area (Δ ABD) = Area (Δ ADC) (∵ median divides the triangle into two triangles of equal areas)

∴ Area (Δ ABD) = Area (Δ ADC) = Area (∆ABC)

Now, consider Δ ABD

Here, BE is the median

Area (Δ ABE) = Area (Δ BED)

∴ Area (Δ ABE) = Area (Δ BED) = Area (∆ABD)

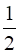Area (Δ BED) = Area (∆ABD)

Area (Δ BED) = 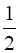× 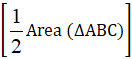(∵Area (Δ ABD) = 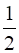Area (∆ABC) )

Area (Δ BED) = Area (∆ABC)

∴ Area (Δ BED) = Area (∆ABC)