In the given figure ABCD is a trapezium in which AB‖DC such that AB = a cm and DC = b cm. If E and F are the midpoints of AD and BC respectively. Then, ar (ABFE) : ar(EFCD) = ?
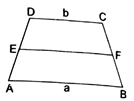
Given: ABCD is a trapezium, AB‖DC, AB = a cm and DC = b cm, E and F are the midpoints of AD and BC.
Since E and F are midpoints of AD and BC, EF will be parallel to both AB and CD.
EF = ![]()
Height between EF and DC and height between EF and AB are equal, because E and F are midpoints OF AD and BC and EF||AB||DC.
Let height between EF and DC and height between EF and AB be h cm.
Area of trapezium = 1/2 × (sum of parallel lines) × height
Now,
Area (Trap.ABFE) = 1/2 × (a + ![]() ) × h.
) × h.
and
Area (Trap.ABFE) = 1/2 × (b + ![]() ) × h.
) × h.
Area (Trap.ABFE) : Area (Trap.ABFE) = 1/2 × (a + ![]() ) × h : 1/2 × (b +
) × h : 1/2 × (b + ![]() ) × h
) × h
Area (Trap.ABFE) : Area (Trap.ABFE) = ![]() :
: ![]() = 3a + b : a + 3b
= 3a + b : a + 3b
∴ Area (Trap.ABFE) : Area (Trap.ABFE) = 3a + b : a + 3b