In the given figure, BD ‖ CA, E is the midpoint of CA and BD = 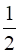CA.
Prove that ar(∆ABC) = 2×ar(∆DBC).

Question

In the given figure, BD ‖ CA, E is the midpoint of CA and BD = CA. Prove that ar(∆ABC) = 2×ar(∆DBC).

Philoid · Accepted Answer

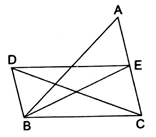
Given: BD ‖ CA, E is the midpoint of CA and BD = CA

Consider Δ BCD and Δ DEC

Here,

BD = EC (∵ E is the midpoint of AC that is CE = 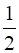CA, BD = 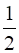CA)

CD = CD (common)

∠BDC = ∠ECD (alternate interior angles, DB||AC)

∴ By SAS congruency

Δ BCD Δ DEC

∴ Area (Δ BCD) = Area (Δ DEC) –1

Here,

Area (Δ BCE) = Area (Δ DEC) (triangles on same base CE and between same parallel lines) –2

E is the midpoint of AC, BE is the median of ΔABC

∴ Area (Δ BCE) = Area (Δ ABE) = 1/2 × Area (Δ ABC)

∴ Area (Δ DEC) = 1/2 × Area (Δ ABC) (∵Area (Δ BCE) = Area (Δ DEC))

∴ Area (Δ BCD) = 1/2 × Area (Δ ABC) (∵Area (Δ DEC) = Area (Δ BCD))

In the given figure, BD ‖ CA, E is the midpoint of CA and BD = CA.Prove that ar(∆ABC) = 2×ar(∆DBC).