Show that (3, 1) as well as (2, – 2) are the solutions of the equation 3x – y = 8. Find two more solutions. How many solutions can we find?

Question

Philoid · Accepted Answer

The equation is 3x – y = 8

For (3, 1), x = 3 and y = 1

LHS = 3×3 – 1

= 9 – 1

= 8 = RHS

Since, RHS = LHS, therefore, (3, 1) is the solution of the equation 3x – y = 8.

For (2, – 2), x = 2 and y = – 2

LHS = 3×3 – 1

= 9 – 1

= 8 = RHS

Since, RHS = LHS, therefore, (2, – 2) is the solution of the equation 3x – y = 8.

Hence, (3, 1) and (2, – 2) are the solutions of the equation 3x – y = 8.

Now to find two more solutions,

3x – y = 8

⇒ y = 3x – 8

Let x = 1, then, y = 3x – 8

⇒ y = 3×1 – 8

⇒ y = 3 – 8

⇒ y = – 5

Therefore, (1, – 5) is a solution of 3x – y = 8.

Let x = 4, then, y = 3x – 8

⇒ y = 3×4 – 8

⇒ y = 12 – 8

⇒ y = 4

Therefore, (4, 4) is a solution of 3x – y = 8.

Plotting the points we obtain the following graph,

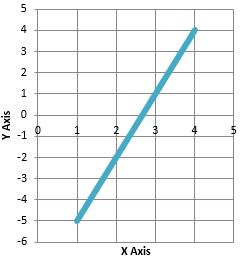
The blue line in the graph is of the equation 3x – y = 8.

From the graph, it is clear that it has infinitely many solutions.