Match the following columns:

Column I	Column II
A. Any line parallel to x-axis is	(p) 3
B. Any line parallel to y-axis is	(q) y = mx
C. Any line passing through the origin is	(r) x = k
D. If the point ( – 2, 2) lies on the line ax + 4y = 2, then a =	(s) y = k

The correct answer is:

(a) – ……., (b) – ……., (c) – ……., (d) – …….,

(a) – (s), (b) – (r), (c) – (q), (d) – (p)

A. We know that the equation of x-axis is y = 0 and the equation of any line parallel to x axis is y = k, where k is any constant.

B. We know that the equation of y-axis is x = 0 and the equation of any line parallel to y axis is x = k, where k is any constant.

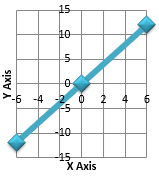
C. For, y = mx

If we put x = 0 then, y = m×0 = 0 therefore, we get (0, 0) which is origin. So, y = mx represents a line passing through the origin.

The blue line is the graph of y = mx which clearly, passes through origin.

D. Given equation, ax + 4y = 2

⇒ ax = 2 – 4y

Point ( – 2,2) i.e, x = – 2 and y = 2

⇒ a = 3