Find whether the given statement is true or false:
(i) x = 2, y = 3 is a solution of the equation 5x – 3y = 1.
(ii) y = 2x + 5 is a straight line passing through the point (1, 5).
(iii) The area bounded by the line x + y = 6, the x-axis and the y-axis is 18 sq units.
(i) Given equation, 5x – 3y = 1
Putting x = 2 and y = 3 in 5x – 3y = 1
LHS = 5x – 3y
= 5× 2 – 3× 3
= 10 – 9
= 1 = RHS
Therefore, the statement is true
(ii) Given equation, y = 2x + 5
Putting x = 1 and y = 5 in y = 2x + 5
⇒ y = 2× 1 + 5
⇒ y = 2 + 5
⇒ y = 7 ≠ 5
Therefore, the statement is false
(iii) Given equation,
x + y = 6
⇒ y = 6 – x
When x = 0, then,
y = 6 – x
⇒ y = 6 – 0
⇒ y = 6
When x = 3, then,
y = 6 – x
⇒ y = 6 – 3
⇒ y = 3
When x = 6, then,
y = 6 – x
⇒ y = 6 – 6
⇒ y = 0
Thus we have the following table,
X | 0 | 3 | 6 |
Y | 6 | 3 | 0 |
Now on plotting (0, 6), (3, 2) and (6, 0) we have the following graph,
Clearly from the graph,
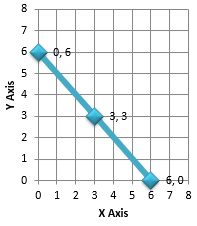
Base of triangle = 6 – 0 = 6 units
Height of triangle = 6 – 0 = 6 units
We know that, Area of triangle =
![]()
![]()
![]()
= 18 sq. units
Therefore, the area of the triangle is 18 sq. units
Therefore, the statement is true