If tanθ = 1/√7 , show that 
We have, tanθ = k/(k√7) = BC/AC (For some value of k)
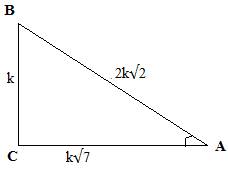
By Pythagoras theorem, (hypotenuse)2 = (perpendicular)2 + (base)2
∴AB2 = BC2 + AC2
= AB2 = (k)2 + (k√7)2
= AB2 = k2 + 7k2
= 8k2 = (2k√2)2
→ AB = 2k√2
∴ cosecθ = AB/BC = 2k√2
secθ = AB/AC = ![]() =
= ![]()
consider the LHS,
LHS = 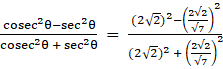
= 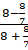
= ![]()
= 48/64
= 3/4
= RHS
HENCE PROVED
11