In the given figure, the chord AB of the larger of the two concentric circles, with center O, touches the smaller circle at C. Prove that AC = CB.

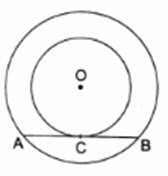
Given: Two concentric circles with common center as O

To Prove: AC = CB

Construction: Join OC, OA and OB

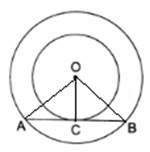
Proof :

OC ⏊ AB

[Tangent at any point on the circle is perpendicular to the radius through point of contact]

In △OAC and △OCB, we have

OA = OB

[∵ radii of same circle]

OC = OC

[∵ common]

∠OCA = ∠OCB

[∵ Both 90° as OC ⏊ AB]

△OAC ≅ △OCB

[By Right Angle - Hypotenuse - Side]

AC = CB

[Corresponding parts of congruent triangles are congruent]

Hence Proved.