In the given figure, an isosceles triangle ABC, with AB = AC, circumscribes a circle. Prove that the point of contact P bisects the base BC.
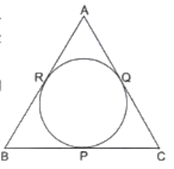
As we know that tangents drawn from an external point to a circle are equal,
BR = BP [ Tangents from point B] [1]
QC = CP [ Tangents from point C] [2]
AR = AQ [ Tangents from point A] [3]
As ABC is an isosceles triangle,
AB = BC [Given] [4]
Now substract [3] from [4]
AB - AR = BC - AQ
BR = QC
BP = CP [ From 1 and 2]
∴ P bisects BC
Hence Proved.
10