In the given figure, PA and PB are two tangents drawn from an external point P to a circle with center C and radius 4 cm. If PA ⏊ PB, then the length of each tangent is

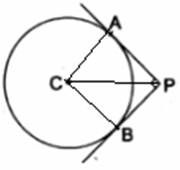
Join AC, BC and CP
To Find: Length of tangents
Now,
PA = PB…[1]
[Tangents drawn at a point on circle is perpendicular to the radius through point of contact]
In △ACP and △BCP
PA = PB [By 1]
CP = CP [Common]
CA = CB [radii of same circle]
△ACP ≅△BCP [By Side - Side - Side Criterion]
∠CPA = ∠CPB
[Corresponding parts of congruent triangles are congruent]
Now,
∠APB = 90°
[Given that PA ⏊ PB]
∠CPA + ∠CPB = 90°
∠CPA + ∠CPA = 90°
2 ∠CPA = 90°
∠CPA = 45°
In △ACP
CA ⏊ PA [Tangents drawn at a point on circle is perpendicular to the radius through point of contact
∴ ACP is a right - angled triangle.
So, we have
![]()
![]()
![]()
⟹PA = 4 cm
From [1]
PA = PB = 4 cm
i.e. length of each tangent is 4 cm