To draw a pair of tangents to a circle, which is inclined to each other at an angle of 45°, we have to draw tangents at the end points of those two radii, the angle between which is

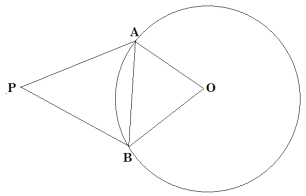
Let us consider a circle with center O and PA and PB are two tangents from point P, given that angle of inclination i.e. ∠APB = 45°

As PA and PB are tangents to given circle,

We have,

OA ⏊ PA and OB ⏊ PB [Tangents drawn at a point on circle is perpendicular to the radius through point of contact]

So, ∠OAP = ∠OBP = 90°

In quadrilateral AQRP,

By angle sum property of quadrilateral, we have

∠OAP + ∠OBP + ∠ABP + ∠AOB = 360°

90° + 90° + 45° + ∠AOB = 360°

∠AOB = 135°