On dividing 3x3 + x2 + 2x + 5 by a polynomial g(X), the quotient and remainder are (3x – 5) and (9x + 10) respectively. Find g(x).
We know that,
According to the division rule, we have
Dividend = Quotient × Divisor + Remainder
Here, we have:
Dividend = 3x3 + x2 + 2x + 5
Quotient = 3x – 5
Remainder = 9x + 10
Putting these values in the formula, we get
3x3 + x2 + 2x + 5 = 3x – 5 × g (x) + 9x + 10
3x3 + x2 + 2x + 5 – 9x – 10 = (3x – 5) × g(x)
3x3 + x2 – 7x – 5 = (3x – 5) × g (x)
g (x) = ![]()
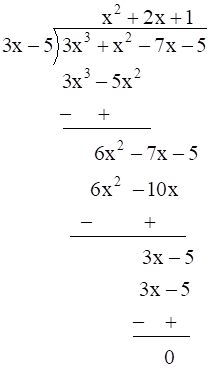
∴ g (x) = x2 + 2x + 1
10