If the median of the following frequency distribution is 32.5, find the values of f₁ and f₂

Class interval	0 - 10	10 - 20	20 - 30	30 - 40	40 - 50	50 - 60	60 - 70	Total
Number of batsmen	f1	5	9	12	f2	3	2	40

Given: Median = 32.5 & N = 40

Assume

Σf_i = N = Sum of frequencies,

h = length of median class,

l = lower boundary of the median class,

f = frequency of median class

and C_f = cumulative frequency

Lets form a table, where x is the unknown frequency.

Median = 32.5 (as already mentioned in the question)

32.5 lies between 30 - 40 ⇒ Median class = 30 - 40

∴ l = 30, h = 10, f = 12, N/2 = (31 + f₁ + f₂)/2 = 40/2 and C_f = 14 + f₁

Median is given by,

⇒

⇒

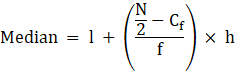
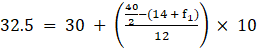
⇒ 32.5 – 30 = (60 – 10f₁)/12

⇒ (2.5)(12) = 60 – 10f₁

⇒ 30 = 60 – 10f₁

⇒ f₁ = 3 …(i)

And given that N = 40

⇒ 31 + f₁ + f₂ = 40

⇒ f₁ + f₂ = 9 …(ii)

Substituting f₁ = 3 in eq.(ii),

3 + f₂ = 9

⇒ f₂ = 6

Thus, the unknown frequencies are f₁ = 3 and f₂ = 6.