Find the mode, median and mean for the following data:
Marks obtained | 25 - 35 | 35 - 45 | 45 - 55 | 55 - 65 | 65 - 75 | 75 - 85 |
Number of students | 7 | 31 | 33 | 17 | 11 | 1 |
To find mean, we will solve by direct method:
CLASS | MID - POINT(xi) | FREQUENCY(fi) | fixi |
25 - 35 | 30 | 7 | 210 |
35 - 45 | 40 | 31 | 1240 |
45 - 55 | 50 | 33 | 1650 |
55 - 65 | 60 | 17 | 1020 |
65 - 75 | 70 | 11 | 770 |
75 - 85 | 80 | 1 | 80 |
TOTAL | 100 | 4970 |
We have got
Σfi = 100 & Σfixi = 4970
∵ mean is given by
![]()
⇒ ![]()
⇒ ![]()
To find median,
Assume Σfi = N = Sum of frequencies,
h = length of median class,
l = lower boundary of the median class,
f = frequency of median class
and Cf = cumulative frequency
Lets form a table.
CLASS | FREQUENCY(fi) | Cf |
25 - 35 | 7 | 7 |
35 - 45 | 31 | 7 + 31 = 38 |
45 - 55 | 33 | 38 + 33 = 71 |
55 - 65 | 17 | 71 + 17 = 88 |
65 - 75 | 11 | 88 + 11 = 99 |
75 - 85 | 1 | 99 + 1 = 100 |
TOTAL | 100 |
So, N = 100
⇒ N/2 = 100/2 = 50
The cumulative frequency just greater than (N/2 = ) 50 is 71, so the corresponding median class is 45 - 55 and accordingly we get Cf = 38(cumulative frequency before the median class).
Now, since median class is 45 - 55.
∴ l = 45, h = 10, f = 33, N/2 = 50 and Cf = 38
Median is given by,
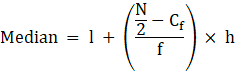
⇒ ![]()
= 45 + 3.64
= 48.64
And we know that,
Mode = 3(Median) – 2(Mean)
= 3(48.64) – 2(49.7)
= 145.92 – 99.4
= 46.52
Hence, mean is 49.7, median is 48.64 and mode is 46.52.