Look at the frequency distribution table given below:
Class interval | 35 - 45 | 45 - 55 | 55 - 65 | 65 - 75 |
Frequency | 8 | 12 | 20 | 10 |
The median of the above distribution is
To find median,
Assume Σfi = N = Sum of frequencies,
h = length of median class,
l = lower boundary of the median class,
f = frequency of median class
and Cf = cumulative frequency
Lets form a table.
CLASS INTERVAL | FREQUENCY(fi) | Cf |
35 - 45 | 8 | 8 |
45 - 55 | 12 | 8 + 12 = 20 |
55 - 65 | 20 | 20 + 20 = 40 |
65 - 75 | 10 | 40 + 10 = 50 |
TOTAL | 50 |
So, N = 50
⇒ N/2 = 50/2 = 25
The cumulative frequency just greater than (N/2 = ) 25 is 40, so the corresponding median class is 55 - 65 and accordingly we get Cf = 20(cumulative frequency before the median class).
Now, since median class is 55 - 65.
∴ l = 55, h = 10, f = 20, N/2 = 25 and Cf = 20
Median is given by,
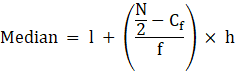
⇒ ![]()
= 55 + 2.5
= 57.5
Thus, median age is 57.5.