Solve for x and y: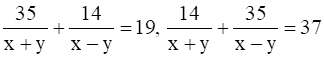

Let us put and.

On substituting these values in the given equations, we get

35p + 14q = 19 … (1)

14p + 35q = 37 … (2)

We know that the general form for a pair of linear equations in 2 variables x and y is a₁x + b₁y + c₁ = 0

and a₂x + b₂y + c₂ = 0.

Comparing with above equations,

we have a₁ = 35, b₁ = 14, c₁ = - 19; a₂ = 14, b₂ = 35, c₂ = - 37

We can solve by cross multiplication method using the formula

Substituting values in the formula, we get

⇒

⇒

⇒ and

⇒ p = 1/7 and q = 1

Since

⇒

⇒ x + y = 7 … (3) and x – y = 1 … (4)

Adding equations (3) and (4),

(x + x) + (y – y) = 7 + 1

2x = 8

x = 4

Substituting x value in (4),

4 – y = 1

y = 3

The solution is x = 4 and y = 3.