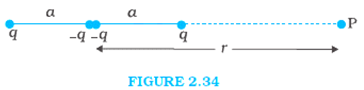
Figure 2.34 shows a charge array known as an electric quadrupole. For a point on the axis of the quadrupole, obtain the dependence of potential on r for r/a >> 1, and contrast your results with that due to an electric dipole, and an electric monopole (i.e., a single charge).

Question

Philoid · Accepted Answer

The diagram is given as:

X Y Z

The given charges of same magnitude placed at points X, Y, and Z respectively, forms an electric quadrupole.

Where, charge + q is at point X, charge -2q is at point Y, and charge + q is at point Z.

The point P is at a distance r from point Y.

Here, XY = YZ = a

So, YP = r, PX = r + a, PZ = r-a.

The electrostatic potential due to the system of three charges at point P is given by,

∴

⇒

Since, r/a>>1

Then a/r<<1 which implies a²/r² is negligible so it can be ignored,

Thus, potential becomes,

V =

Relation of potential due to quadrupole with r is V1/r³

However, for a dipole it is V1/r²

And for a monopole it is V1/r