Obtain the equivalent capacitance of the network in Fig. 2.35. For a 300 V supply, determine the charge and voltage across each capacitor.

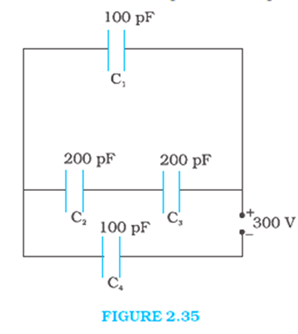
Capacitance of capacitor C₁ = 100pF, C2 = 200pF, C3 = 200 pF, C4 = 100 pF.

Supply potential (V) = 300 V

Let the equivalent capacitance of capacitors C₂ and C₃(connected in series) be C'.

⇒ C’ = 100pF

Let the equivalent capacitance of capacitors C₁ and C’(connected in parallel) be C’’.

C’’ = C’ + C₁ = 100 + 100 = 200pF

Let the equivalent capacitance of C’’ and C4 (connected in series) be C’’’.

⇒ C’’’ = 200/3pF

Thus, the equivalent capacitance of the circuit = 200/3 pF.

Now, Supply potential (V) = 300 V

Charge on C₄ is given by,

Q₄ = C’’’V = = 2 × 10^-8C

So, V₄ = Q₄/C₄ = (210^-8)/(10010^-12) = 200C

Potential difference across C₁ is given by, V1 = V-V₄ = 300-200 = 100V

Charge on C₁ is given by, Q1 = C₁V₁ = 100 × 10^-12 × 100 = 10^-8C

C₂ and C₃ having same capacitances have a potential difference of 100 V together.

Since C₁ and C₃ are in series, the potential difference across C₂ and C₃ is given by,V₂ = V₃ = 50V

Therefore charge on C₂ is given by,Q₂ = C₂V₂ = 20010^-1250 = 10^-8C

And charge on C₃ is given by,Q₃ = C₃V₃ = 20010^-1250 = 10^-8C.

The charge and voltage across each capacitor are as follows: