A solid right circular cone is cut into two parts at the middle of its height by a plane parallel to its base. The ratio of the volume of the smaller cone to the whole cone is

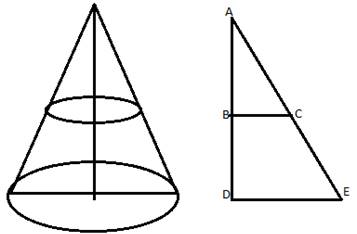
Given: A solid right circular cone is cut into two parts at the middle of its height by a plane parallel to its base

Let ‘H’ be the height of the cone.

Let ‘R’ be the Radius of the complete cone.

Volume of a cone is given by: πr²h

Here,

AB = BD =

Let r be the radius of the smaller cone.

∴ In ΔABC and ΔADE

∠ABC = ADE (90°)

∠CAB = ∠EAB (common)

∴ ΔABC ΔADE (AA similarity criterion)

⇒ = (Corresponding sides are proportional)

⇒ =

⇒ R = 2r

Volume of smaller cone = π(r)² × h = π(BC)² × AB = π(r)² × = cm³

Volume of whole cone = π(r)² × h = π(DE)² × AD = π(2r)² × H = πr²H cm³

∴ = =

∴ The ratio of the volume of the smaller cone to the whole cone is 1:8