The radii of the circular end of a solid frustum of a cone are 33 cm and 27 cm and its slant height is 10 cm. Find its capacity and total surface area. [Take π = 22/7.]
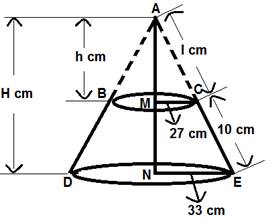
fig.23
Given –
MC = 27 cm, NE = 33 cm and CE = 10 cm
Let AM = h cm, AN = H cm and AC = l cm
∴ AE = AC + CE = (l + 10) cm
In the above fig.19,
Δ AMC and Δ ANE are similar triangles because their corresponding angles are equal.
![]()
![]() …..(1)
…..(1)
On cross multiplying last two fractional parts of equation(1), we get –
33l = 27l + 270
⇒ 6l = 270
∴ l = 45 cm
∴ AE = 45 + 10 = 55 cm
In Δ ANE,
AN2 + NE2 = AE2 [by using pythagoras theorem]
⇒ H2 + (33)2 = (55)2
⇒ H2 + 1089 = 3025
⇒ H2 = 1936
∴ H = 44 cm
From first and last fractional parts of equation(1), we get –
h = (27/33) × 44 = 36 cm
∴ Height of frustum = H – h = 44 – 36 = 8 cm
Now,
Capacity of Frustum = Vol. of Cone ADE – Vol. of cone ABC
= (1/3)π × (NE)2 × (AN) – (1/3)π × (MC)2 × (AM)
= (1/3)π × [(33)2 × (44) – (27)2 × (36)]
= (22/21) × [47916 – 26244]
= (22/21) × 21672
= 22 × 1032
= 22704 cm3
Total Surface Area of Frustum
= Area of Curved Part(Trapezium)
+ Area of Upper Circular Part
+ Area of lower Circular Part
= [(1/2) × (sum of parallel sides) × (height of frustum)]
+ [π × (MC)2] + [π × (NE)2]
= [(1/2) × 2π(27 + 33) × 8] + [(22/7) × (27)2] + [(22/7) × (33)2]
= 480(22/7) + (22/7) × [(27)2 + (33)2]
= 480(22/7) + (22/7) × 1818
= (22/7) × 2298
= 22 × 328.28
= 7222.16 cm2
Thus, Capacity of Frustum = 22704 cm3
and, Total Surface Area of Frustum = 7222.16 cm2