Find the area of the minor segments of a circle of radius 14 cm, when its central angle is 60°. Also find the area of the corresponding major segment. (Use π = 22/7)

Question

Philoid · Accepted Answer

The figure represents the problem

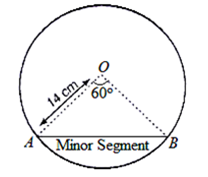
With AO and OB as radius

Now as

OA = AB (radii of same circle)

∠OBA = ∠OAB (Angles opposite to equal sides are equal)

Also

In △AOB

∠AOB + ∠OBA + ∠OAB = 180°

60 + ∠OBA + ∠OBA = 180°

2∠OBA = 120°

∠OBA = 60°

So, We have

∠OBA = ∠OAB = ∠AOB = 60°

So AOB is an equilateral triangle with side 14 cm [radius of circle]

And as we know

Where a = side of triangle

Area of minor segment = area of minor sector OAB - ar(△OAB)

Area of major segment = area of circle - area of minor segment