In figure 5, PQRS is a square lawn with side PQ = 42 meters. Two circular flower beds are there on the sides PS and PQ with center at O, the intersection of its diagonals. Find the total area of the two flower beds (shaded parts).
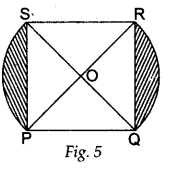
The figure is given as:

Since the lawn is a square, ∴ the sides PQ = QR = SR = SP = 42 m.
Also, let OR = OP = x being the radius of the circle.
Now, the diagonal PR = OR + OP = x + x = 2x.
Applying the Pythagoras theorem in ΔPRQ, we get,
(PR)2 = (RQ)2 + (PQ)2
⇒ (2x)2 = (42)2 + (42)2
⇒ 4x2 = 2× (42)2
⇒ x2 = 882
⇒ x = √882 = 21√2 m.
Now, Area of the two flower beds = 2× {Area of the segment of circle with centre angle 90°)
⇒ Area ![]()
⇒ ![]()
⇒ A = 2{ 693 – 441} = 504 m2
∴ Area of the flowers beds is 504 m2
30