Prove that the parallelogram circumscribing a circle is a rhombus.

Question

Philoid · Accepted Answer

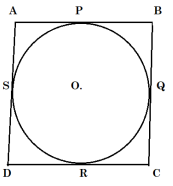
Consider a circle circumscribed by a parallelogram ABCD, Let side AB, BC, CD and AD touch circles at P, Q, R and S respectively.

To Proof : ABCD is a rhombus.

As ABCD is a parallelogram

AB = CD and BC = AD [opposite sides of a parallelogram are equal] …[1]

Now, As tangents drawn from an external point are equal.

We have

AP = AS [tangents from point A]

BP = BQ [tangents from point B]

CR = CQ [tangents from point C]

DR = DS [tangents from point D]

Add the above equations

AP + BP + CR + DR = AS + BQ + CQ + DS

⇒ AB + CD = AS + DS + BQ + CQ

⇒ AB + CD = AD + BC

⇒ AB + AB = BC + BC [From 1]

⇒ AB = BC …[2]

From [1] and [2]

AB = BC = CD = AD

And we know,

A parallelogram with all sides equal is a rhombus

So, ABCD is a rhombus.

Hence Proved !