In the given figure ΔABC is right angled at A. Semicircles are drawn on AB, AC and BC as diameter. It is given that AB = 3 cm and AC = 4 cm. Find the area of the shaded region.
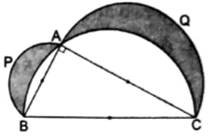
Let semicircle I, II and III are semicircles with diameters AB, AC and BC respectively
Area of shaded region =
Area of semicircle I + Area of semicircle II + Area of triangle ABC – Area of semicircle III
As, ∠BAC is in semicircle,
∠BAC = 90° [Angle in a semicircle is right angle]
And ABC is a right – angled triangle at A
By Pythagoras Theorem
(Hypotenuse)2 = (Base)2 + (Perpendicular)2
(BC)2 = (AB)2 + (AC)2
⇒ (BC)2 = 32 + 42 = 9 + 16 = 25
⇒ BC = 5 cm
Now, For semicircle I
Diameter = AB = 3 cm
Radius![]()
Area of semicircle of radius r![]()
Area of semicircle I![]()
For semicircle II
Diameter = AC = 4 cm
Radius![]()
Area of semicircle of radius r![]()
Area of semicircle II![]()
For semicircle III
Diameter = BC = 5 cm
Radius,![]()
Area of semicircle of radius r ![]()
Area of semicircle I ![]()
Area of a right – angled triangle![]()
Area of ΔABC![]()
Required area (From eqn [1])![]()