Consider a binary operation ∗ on the set {1, 2, 3, 4, 5} given by the following multiplication table (Table 1.2).
(i) Compute (2 ∗ 3) ∗ 4 and 2 ∗ (3 ∗ 4)
(ii) Is ∗ commutative?
(iii) Compute (2 ∗ 3) ∗ (4 ∗ 5).
(Hint: use the following table)
Table 1.2
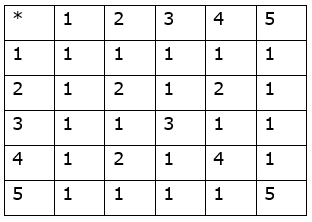
(i) (2 ∗ 3) ∗ 4 = 1 * 4 = 1
2 ∗ (3 ∗ 4) = 2 * 1 = 1
(ii) For every a, b ϵ {1, 2, 3, 4, 5},
We have, a * b = b * a
⇒ the operation * is commutative.
(iii) (2 ∗ 3) = 1
⇒ (2 ∗ 3) ∗ (4 * 5) = 1 * 1 = 1
4