Let f: R → R be the Signum Function defined as

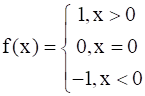
and g: R → R be the Greatest Integer Function given by g(x) = [x], where [x] is greatest integer less than or equal to x. Then, does fog and gof coincide in (0, 1]?

Question

Philoid · Accepted Answer

It is given that

f: R → R be the Signum Function defined as

Also, g: R → R is defined as g(x) = [x], where [x] is the greatest integer less than or equal to x.

Now, let x ϵ (0, 1]

Then, we get,

[x] = 1 if x = 1 and [x] = 0 if 0 < x < 1

Therefore, fog(x) = f(g(x)) = f([x]) =

gof(x) = g(f(x))

= g(1) [x > 0]

= [1] = 1

Then, when x ϵ (0,1), we get fog(x) = 0 and gof(x) = 1

But fog(1) ≠ gof(1)

Therefore, fog and gof do not coincide in (0, 1].

Let f: R → R be the Signum Function defined asand g: R → R be the Greatest Integer Function given by g(x) = [x], where [x] is greatest integer less than or equal to x. Then, does fog and gof coincide in (0, 1]?