Find all points of discontinuity of f, where f is defined by

Question

Philoid · Accepted Answer

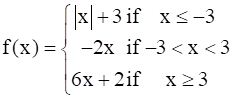
The given function is

The function f is defined at all points of the real line.

Let k be the point on a real line.

Then, we have 5 cases i.e., k < -3, k = -3, -3 < k < 3, k = 3 or k > 3

Now, Case I: k < -3

Then, f(k) = -k + 3

= -k + 3= f(k)

Thus,

Hence, f is continuous at all real number x < -3.

Case II: k = -3

f(-3) = -(-3) + 3 = 6

=-(-3) + 3 = 6

= -2×(-3) = 6

Hence, f is continuous at x = -3.

Case III: -3 < k < 3

Then, f(k) = -2k

= -2k = f(k)

Thus,

Hence, f is continuous in (-3,3).

Case IV: k = 3

= -2×(3) = -6

= 6 × 3 + 2 = 20

Hence, f is not continuous at x = 3.

Case V: k > 3

Then, f(k) = 6k + 2

= 6k + 2= f(k)

Thus,

Hence, f is continuous at all real number x < 3.

Therefore, x = 3 is the only point of discontinuity of f.