Find all points of discontinuity of f, where

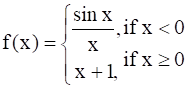
It is given that

We know that f is defined at all points of the real line.

Let k be a real number.

Case I: k < 0,

Then f(k) =

Thus, f is continuous at all points x that is x < 0.

Case II: k > 0,

Then f(k) = c + 1

Thus, f is continuous at all points x that is x > 0.

Case III: k = 0

Then f(k) = f(0) = 0 + 1 = 1

= 1

= 1

Hence, f is continuous at x = 0.

Therefore, f is continuous at all points of the real line.