Examine the continuity of f, where f is defined by

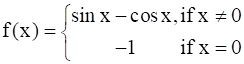
It is given that

We know that f is defined at all points of the real line.

Let k be a real number.

Case I: k ≠ 0,

Then f(k) = sink - cosk

Thus, f is continuous at all points x that is x ≠ 0.

Case II: k = 0

Then f(k) = f(0) = 0

Therefore, f is continuous at x = 0.

Therefore, f has no point of discontinuity.