Find the values of k so that the function f is continuous at the indicated point in Exercises 26 to 29.

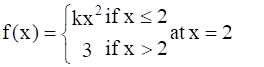
It is given that

Also, it is given that function f is continuous at x = 2,

So, if f is defined at x = 2 and if the value of the f at x = 2 equals the limit of f at x = 2.

We can see that f is defined at x = 2 and

f(2) = k(2)² = 4k

⇒

⇒ k × 2² = 3 = 4k

⇒ 4k = 3 = 4k

⇒ 4k = 3

⇒ k =

Therefore, the required value of k is .