Express the following matrices as the sum of a symmetric and a skew symmetric matrix:

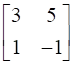
As per Theorem 2 “Any square matrix can be expressed as the sum of a symmetric and skew symmetric matrix.” So in order to prove this we will be using Theorem 1 which states that “For any square matrix A with real number entries, A + A’ is a symmetric matrix and A – A’ is a skew symmetric matrix.”

Now, on adding A and A’ we will get,

.

.

.

.

on subtracting A’ from A we will get,

Now, Add M and N, we get,

.

us, A is represented as the sum of a symmetric matrix M and a skew symmetric matrix N.

Ans. Hence proved