Using elementary transformations, find the inverse of each of the matrices.

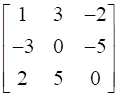
First of all we need to check whether the matrix is invertible or not. For that-

For the inverse of a matrix A to exist,

Determinant of A ≠ 0

Here ∣A∣ = [ (1) {0- 5 × (-5)} – (3) {(-3) × 0 – (-5) × 2} + (-2) {5 × (-3) – 2 × 0}]

= [1 {25} - 3 {0 + 10} - 2 {-15}]

= [1(25) - 3(10) – 2 (-15)]

= [25-30+30]

= 25

So the matrix is invertible.

Now to find the inverse of the matrix,

We know AA^-1 = I

Let’s make augmented matrix-

→ [A : I]

→

Apply row operation- R₂→ R₂ + 3R₁

→

Apply row operation- R₃→ R₃ -2R₁

→

Apply row operation- R₂→ R₂

→

Apply row operation- R₁→ R₁ – 3R₂

→

Apply row operation- R₃→ R₃ + R₂

→

Apply row operation- R₁→ R₁ - R₃

→

Apply row operation- R₂→ R₂ + R₃

→

Apply row operation- R₃→ R₃

→

The matrix so obtained is of the form –

→ [I : A^-1]

Hence inverse of the given matrix-

→