If u, v and w are functions of x, then show that

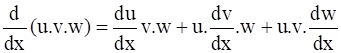
in two ways – first by repeated application of product rule, second by logarithmic differentiation.

To prove:

Let y=u.v.w=u.(v.w)

(a) by applying product rule differentiate both sides with respect to x

(b) Taking log on both sides, we get

as, y=u.v.w

log y = log (u.v.w)

log y = log u + log v + log w

Now, differentiate both sides with respect to x