Write Minors and Cofactors of the elements of following determinants:

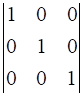
Minor of an element a_ij = M_{ij �}

a₁₁ = 1, Minor of element a₁₁ = M₁₁ = = (1 × 1) – (0 × 0) = 1

Here removing 1^st row and 1^st column from the determinant we are left out with the determinant. Solving this we get M₁₁ = 1

Similarly, finding other Minors of the determinant

a₁₂ = 0, Minor of element a₁₂ = M₁₂ = = (0 × 1) – (0 × 0) = 0

a₁₃ = 0, Minor of element a₁₃ = M₁₃ = = (0 × 0) - (1 × 0) = 0

a₂₁ = 0, Minor of element a₂₁ = M₂₁ = = (0 × 1) – (0 × 0) = 0

a₂₂ = 1, Minor of element a₂₂ = M₂₂ = = (1 × 1) – (0 × 0) = 1

a₂₃ = 0, Minor of element a₂₃ = M₂₃ = = (1 × 0) – (0 × 0) = 0

a₃₁ = 0, Minor of element a₃₁ = M₃₁ = = (0 × 0) – (0 × 1) = 0

a₃₂ = 0, Minor of element a₃₂ = M₃₂ = = (1 × 0) – (0 × 0) = 0

a₃₃ = 1, Minor of element a₃₃ = M₃₃ = = (1 × 1) – (0 × 0) = 1

Cofactor of an element a_ij, A_ij = (-1)^i+j × M_ij

A₁₁ = (-1)¹⁺¹ × M₁₁ = 1 × 1 = 1

A₁₂ = (-1)¹⁺² × M₁₂ = (-1) × 0 = 0

A₁₃ = (-1)¹⁺³ × M₁₃ = 1 × 0 = 0

A₂₁ = (-1)²⁺¹ × M₂₁ = (-1) × 0 = 0

A₂₂ = (-1)²⁺² × M₂₂ = 1 × 1 = 1

A₂₃ = (-1)²⁺³ × M₂₃ = (-1) × 0 = 0

A₃₁ = (-1)³⁺¹ × M₃₁ = 1 × 0 = 0

A₃₂ = (-1)³⁺² × M₃₂ = (-1) × 0 = 0

A₃₃ = (-1)³⁺³ × M₃₃ = 1 × 1 = 1