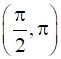Show that the function given by f (x) = sin x is

(a) strictly increasing in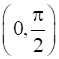

(b) strictly decreasing in

(c) neither increasing nor decreasing in (0, π)

(a) The function is f (x) = sin x

Then, f’(x) = cos x

Since for each x ϵ , cos x > 0, we have f’(x) > 0

Therefore, f’ is strictly increasing in.

(b) The function is f (x) = sin x

Then, f’(x) = cos x

Since for each , cos x < 0, we have f’(x) < 0

Therefore, f’ is strictly decreasing in.

(c) The function is f (x) = sin x

Then, f’(x) = cos x

Since for each x ϵ , cos x > 0, we have f’(x) >0

Therefore, f’ is strictly increasing in……………….(1)

Now, The function is f (x) = sin x

Then, f’(x) = cos x

Since, for each x ϵ, cos x < 0, we have f’(x) < 0

Therefore, f’ is strictly decreasing in …………(2)

From (1) and (2),

It is clear that f is neither increasing nor decreasing in (0, π).