Find points on the curve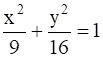 
at which the tangents are
(i) parallel to x-axis (ii) parallel to y-axis.
(i) It is given that 
Now, differentiating both sides with respect to x, we get
We know that the tangent is parallel to the x –axis if the slope is 0 ie,
, which is possible if x =0
Then, 
for x =0
⇒ y2 = 16
⇒ 
Therefore, the points at which the tangents are parallel to the x-axis are (0,4) and (0, -4).
(ii) It is given that 
Now, differentiating both sides with respect to x, we get
We know that the tangent is parallel to the y–axis if the slope of the normal is 0 ie,
,
⇒ y = 0
Then, 
for y =0
⇒ 
Therefore, the points at which the tangents are parallel to the y-axis are (3,0) and (-3,0).
13